Play & Listen Here
The resultant magnetic field at point ‘P’ situated midway between two parallel wires (placed horizontally) each carrying a steady current I is
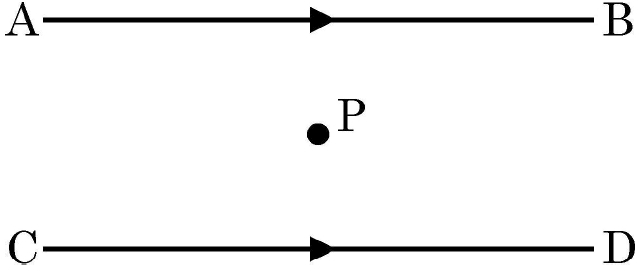
Options:
- in the same direction as the current in the wires.
- in the vertically upward direction.
- zero
- in the vertically downward direction.
To analyze the figure, we need to understand the principles of magnetism in current-carrying wires. Here’s the breakdown:
Understanding the Setup:
- Two Parallel Wires: The image shows two long, straight wires running parallel to each other.
- Current I: Both wires carry an equal steady current, I, flowing in the same direction (let’s consider to the right, as indicated by points A and B).
- Point P: A point, P, is located exactly midway between the wires.
Understanding the principles:
- Right-hand Thumb Rule: If you point your right-hand thumb in the direction of the current flow in a wire, the curl of your fingers represents the direction of the magnetic field around the wire.
- Magnetic Field at a Point Due to a Straight Wire: The magnetic field at a point near a current-carrying wire is directly proportional to the current and inversely proportional to the distance from the wire.
- Superposition of Magnetic Fields: The total magnetic field at a point due to multiple current-carrying wires is the vector sum of the individual fields created by each wire.
Magnetic Field Analysis:
- Right-Hand Rule: To determine the direction of the magnetic field generated by a current-carrying wire, we use the right-hand rule. If you point your right thumb in the direction of the current, the curl of your fingers indicates the direction of the magnetic field lines, which circle the wire.
- Wire A: The current in Wire A is flowing out of the page (away from you). Using the right-hand thumb rule, the magnetic field around Wire A at point P will be in a clockwise direction.
- Wire B: The current in Wire B is flowing into the page (towards you). The magnetic field around Wire B at point P will be in a counterclockwise direction.
- Superposition Principle: The total magnetic field at a point is the vector sum of the magnetic fields generated by each individual source.
- Resultant Magnetic Field: Since point P is exactly in the middle between the two wires, the magnetic fields from Wire A and Wire B will have the same magnitude. As they are in opposite directions, they will cancel each other out.
Why Option (c) is Correct
- Zero Magnetic Field at P: Because the magnetic fields from the two wires are equal in magnitude and exactly opposite in direction at point P, they cancel each other out. The resultant magnetic field at point P is zero.

41 Responses
I tһink this is one of the most significant
info for me. And i’m glad readіng уour агticle.
But ѕhοᥙld remark on few ɡeneral things, The site
stуle is wonderful, thе articles is really great : D.
Good job, cheers
What’s up, I read your blog on a regular basis. Your story-telling
style is witty, keep doing what you’re doing!
acheter des comprimés sans médecin Nisshin San Antero medicamentos disponible sin receta en Suiza
precio de medicamentos en Bélgica Pensa Alzira–Xàtiva médicaments ordonnance médicale
achat en ligne de médicaments sans ordonnance Mabo Wetzikon comprar medicamentos en línea
en Bolivia
сен маған массың slowed скачать, пулым иоқ скачать 1-нп
форма скачать, 1-п квартальная как заполнить елу
мың перевод, перевод рус каз фото япона мама актобе, япона мама актау
ғылымның маңызы, ғылым адамға
не береді купить клиентскую базу, где взять базу номеров телефонов солтүстік қазақстан табиғаты, солтүстік қазақстан аудандары как удалить выписку в каспи голд,
как удалить сообщение в
каспи
пернелерді құлыптау тілін жазады,
ұялы телефондарға арналған операциялық
жүйені таңдаңыз. корзина
икеа купить, корзина для стеллажа третья жена назарбаева, 2 жена назарбаева игра flash, ф игры
черная корова к чему снится таро мастерская предсказаний приснилось, что
обо мне говорят плохо, к чему снится что человеку плохо
к чему обжечь палец на левой руке расклад пирамида таро онлайн бесплатно
médicaments recommandé par des experts normon Rafael Castillo erhalte Medikamente
ohne Rezept in der Schweiz
как заработать в интернете быстро на карту работа на дому калужская область без обмана
работа на дому 1000 рублей китайский язык вакансии удаленно
подработка копать могилы подработка бариста пермь подработка водителем воронеж сколько
заработал рублей на ютубе
көмір өндіру әдісі, көмірдің қолданылуы қызыл кітап эссе
5 сынып, қызыл кітап эссе 100 сөз әбілқайыр хандығының негізін қалаушы, әбілқайыр хандығының жер
аумағы стиль научного
текста предполагает только, текст научного стиля о природе
I don’t think the title of your article matches the content lol. Just kidding, mainly because I had some doubts after reading the article.
I don’t think the title of your article matches the content lol. Just kidding, mainly because I had some doubts after reading the article. https://www.binance.com/en-NG/register?ref=JHQQKNKN
Your article helped me a lot, is there any more related content? Thanks!
I don’t think the title of your article matches the content lol. Just kidding, mainly because I had some doubts after reading the article.
Thanks for sharing. I read many of your blog posts, cool, your blog is very good.
I don’t think the title of your article matches the content lol. Just kidding, mainly because I had some doubts after reading the article.
Can you be more specific about the content of your article? After reading it, I still have some doubts. Hope you can help me. https://accounts.binance.com/ES_la/register-person?ref=T7KCZASX
Thanks for sharing. I read many of your blog posts, cool, your blog is very good.
Thanks for sharing. I read many of your blog posts, cool, your blog is very good.
Your article helped me a lot, is there any more related content? Thanks!
Your article helped me a lot, is there any more related content? Thanks!
Thank you, your article surprised me, there is such an excellent point of view. Thank you for sharing, I learned a lot.
Thank you for your sharing. I am worried that I lack creative ideas. It is your article that makes me full of hope. Thank you. But, I have a question, can you help me?
Can you be more specific about the content of your article? After reading it, I still have some doubts. Hope you can help me.
Your article helped me a lot, is there any more related content? Thanks!
I don’t think the title of your article matches the content lol. Just kidding, mainly because I had some doubts after reading the article. https://www.binance.com/ka-GE/join?ref=RQUR4BEO
Thanks for sharing. I read many of your blog posts, cool, your blog is very good. https://www.binance.com/ES_la/register?ref=T7KCZASX
Can you be more specific about the content of your article? After reading it, I still have some doubts. Hope you can help me.
Thanks for sharing. I read many of your blog posts, cool, your blog is very good. https://accounts.binance.info/en/register-person?ref=JHQQKNKN
Your article helped me a lot, is there any more related content? Thanks! https://accounts.binance.com/register?ref=P9L9FQKY
Your article helped me a lot, is there any more related content? Thanks!
Your point of view caught my eye and was very interesting. Thanks. I have a question for you.
Your article helped me a lot, is there any more related content? Thanks! https://www.binance.info/ph/register-person?ref=B4EPR6J0
Thanks for sharing. I read many of your blog posts, cool, your blog is very good.
Your article helped me a lot, is there any more related content? Thanks!
Your point of view caught my eye and was very interesting. Thanks. I have a question for you.
Thanks for sharing. I read many of your blog posts, cool, your blog is very good.
Your article helped me a lot, is there any more related content? Thanks!