Here’s a breakdown of the question in simple language, along with examples:
Understanding Zeroes:
- Imagine a quadratic polynomial is a road that goes up and down, like a hill.
- The “zeroes” are the points where the road crosses the x-axis, kind of like where the hill meets the ground.
- The question is asking you to build a road (polynomial) that has its “hills” hitting the ground at specific points (zeroes) that have a particular relationship to each other.
Sum and Product of Zeroes:
- The “sum” of the zeroes is what you get when you add them together.
- The “product” of the zeroes is what you get when you multiply them.
- The question gives you these clues about the zeroes: their sum is -3 and their product is 2.
Building the Polynomial:
- To build the polynomial, we use a special pattern: x² – (sum of zeroes)x + (product of zeroes)
- Plugging in the values from the question, we get: x² – (-3)x + 2
- Simplifying, we get the quadratic polynomial: x² + 3x + 2
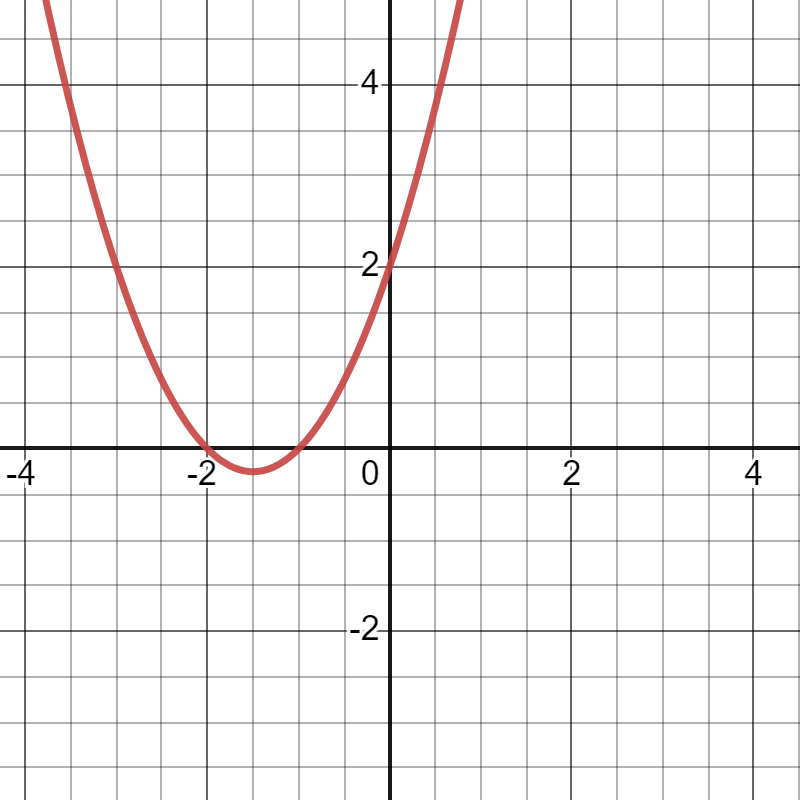
Example with Numbers:
- Imagine the zeroes are -1 and -2.
- Their sum is -1 + (-2) = -3.
- Their product is (-1) x (-2) = 2.
- The polynomial would be x² + 3x + 2.
Key Points:
- The zeroes of a quadratic polynomial are the values of x that make the polynomial equal to zero.
- The sum and product of the zeroes can be found using the coefficients of the polynomial.
- The coefficient of x² is always 1.
- The coefficient of x is the negative of the sum of the zeroes.
- The constant term is the product of the zeroes.
Also Check out other Questions…


Leave a Reply